

Crystal Structures
Why study crystal structures?
The physical properties of solids depend entirely upon the arrangement of the atoms that make up the solid and the distances between them.
The arrangement of the atoms in a crystal structure is a combination of the size and shape of the unit-cell and the arrangement of atoms inside the unit-cell. See our rough guide!
The arrangement of the atoms in a crystal structure is a combination of the size and shape of the unit-cell and the arrangement of atoms inside the unit-cell. See our rough guide!
Arrangement of atoms
The arrangement of atoms within the unit-cell can be described in terms of their fractional coordinates or positions relative to the corners of the unit-cell.
The intensities of the diffracted X-ray beams are related to the atom positions through the structure factor equation:
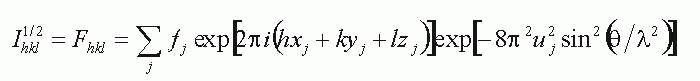
The summation is over all of the atoms in the unit-cell, each labelled by subscript j.
The xyz are the fractional coordinates of the atom, the f is its scattering power of the stationary atom. The u is the "temperature factor", which reduces the measured intensity scattered by the atom because of its thermally-induced vibrational motion.
The hkl is the index of the reflection being measured, at a Bragg angle q with a wavelenth l.
Even if we measure the intensities of many reflections, this equation cannot be directly solved to obtain the xyz and u. This is known as the "phase problem". Its existence keeps crystallographers in jobs because...
We have to "guess" the values of xyz of all of the atoms in the unit-cell and then perform a "structure refinement" in which the positions of the atoms are adjusted until the calculated intensities match the observed ones.
The process of making the initial "guessed" structure is called "structure solution". There are mathematical tools built into software to help us with this process and now make it almost automatic for simple structures. But crystallographic knowledge is required for complex cases, and even simple ones can sometimes fool the software into providing an incorrect structure solution.
Here are the results of a typical structure refinement. It is from a crystal of coesite, a high-pressure polymorph of SiO2. Coesite is found in a few metamorphic rocks which have been buried to depths of more than 100km in the Earth.
The intensities of the diffracted X-ray beams are related to the atom positions through the structure factor equation:
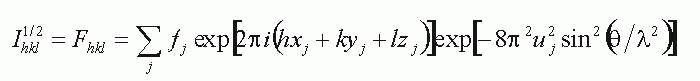
The summation is over all of the atoms in the unit-cell, each labelled by subscript j.
The xyz are the fractional coordinates of the atom, the f is its scattering power of the stationary atom. The u is the "temperature factor", which reduces the measured intensity scattered by the atom because of its thermally-induced vibrational motion.
The hkl is the index of the reflection being measured, at a Bragg angle q with a wavelenth l.
Even if we measure the intensities of many reflections, this equation cannot be directly solved to obtain the xyz and u. This is known as the "phase problem". Its existence keeps crystallographers in jobs because...
We have to "guess" the values of xyz of all of the atoms in the unit-cell and then perform a "structure refinement" in which the positions of the atoms are adjusted until the calculated intensities match the observed ones.
The process of making the initial "guessed" structure is called "structure solution". There are mathematical tools built into software to help us with this process and now make it almost automatic for simple structures. But crystallographic knowledge is required for complex cases, and even simple ones can sometimes fool the software into providing an incorrect structure solution.
Here are the results of a typical structure refinement. It is from a crystal of coesite, a high-pressure polymorph of SiO2. Coesite is found in a few metamorphic rocks which have been buried to depths of more than 100km in the Earth.
|
These are the refined fractional coordinates of the two silicon atoms and five oxygen atoms that make up the structure.
They were determined by refinement to 429 measured reflection intensities. |
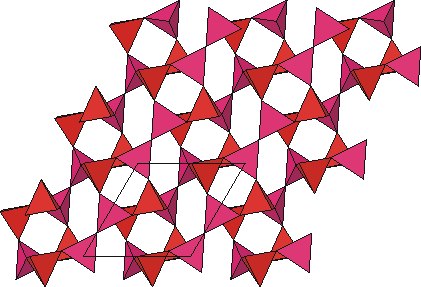
And this is the structure drawn as a polyhedral model. The tetrahedra represent the SiO4 groups in the structure with an oxgen at each corner and a silicon in the center.
The tetrahedra are linked at the corners, representing Si-O-Si linkages in the structure. |
||||||||||||||||||||||||||||||||
|
 |
When the fractional coordinates are combined with the lattice parameters that define the size and shape of the unit-cell, we can calculate the distances between the atoms, or the bond lengths.
For coesite the Si-O bond lengths range from 1.595A to 1.627A at room pressure.
We can also calculate geometric parameters like the angle between two bonds to a given atom.
In coesite at room pressure the Si-O-Si angles at the five different oxygen atoms are:
The numbers in parentheses are the estimated uncertainties in the quantities. They are obtained automatically as part of the mathematical process of structure refinement.
We simply load our crystal into a diamond-anvil cell, apply pressure, and measure the diffracted X-ray intensities from the crystal.
The details of the additional experimental techniques necessary for measuring structures at high pressure can be found in volume 41 of the Reviews in Mineralogy and Geochemistry, available from the MSA.
We have been funded by NSF grant EAR-0105864 to further develop the techniques for determining structures at high pressure. A summary of the project is available as a pdf file.
For coesite the Si-O bond lengths range from 1.595A to 1.627A at room pressure.
We can also calculate geometric parameters like the angle between two bonds to a given atom.
In coesite at room pressure the Si-O-Si angles at the five different oxygen atoms are:
| O1 | O2 | O3 | O4 | O5 |
| 180.0 | 142.5(2) | 144.8(2) | 149.8(2) | 137.4(1) |
The numbers in parentheses are the estimated uncertainties in the quantities. They are obtained automatically as part of the mathematical process of structure refinement.
Structures at high pressure
Why high pressure?
The physical properties of solids can change as the distances between the atoms change. As a simple example, solids become stiffer as the atoms are moved together. We therefore use high pressure as a "clean" way to probe the behaviour and properties of crystals. The application of pressure with diamond-anvil cells forces atoms in a crystal closer together. We measure the changes in the atomic arrangement by X-ray diffraction.
The geological applications of our high-pressure studies of minerals are direct: Minerals within the Earth are subject to high pressures, so with our diamond-anvil experiments we are measuring the minerals in their "natural state".
The geological applications of our high-pressure studies of minerals are direct: Minerals within the Earth are subject to high pressures, so with our diamond-anvil experiments we are measuring the minerals in their "natural state".
We simply load our crystal into a diamond-anvil cell, apply pressure, and measure the diffracted X-ray intensities from the crystal.
The details of the additional experimental techniques necessary for measuring structures at high pressure can be found in volume 41 of the Reviews in Mineralogy and Geochemistry, available from the MSA.
We have been funded by NSF grant EAR-0105864 to further develop the techniques for determining structures at high pressure. A summary of the project is available as a pdf file.
|
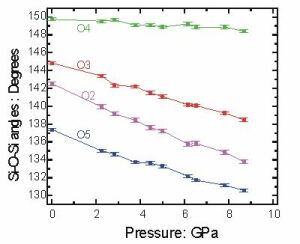
As an example, we have determined the structure of coesite up to nearly 9 GPa in pressure.
Because the Si-O bonds in coesite are strong, they do not change very much with pressure. Instead, the almost rigid polyhedra "tilt" at the corners in order to reduce the volume of the crystal. These tilts are really the Si-O-Si angles at the oxygen atoms, plotted here. Note the surprising result that the smallest angle gets smaller faster than the others. |
 |