Nächste Seite: Orientierungs-Teil Aufwärts: Verfeinerung der Orientierung Vorherige Seite: Verfeinerung der Orientierung Inhalt Index
Die Metrik-Matrix![]() ist eine fiktive Orientierungsmatrix in einer Standardisierten Orientierung (z.B. entlang den Basisvektoren des Laborkoordinatensystems). Sie hat so viele von 0 verschiedene Komponenten, wie der Metrik-Tensor (
ist eine fiktive Orientierungsmatrix in einer Standardisierten Orientierung (z.B. entlang den Basisvektoren des Laborkoordinatensystems). Sie hat so viele von 0 verschiedene Komponenten, wie der Metrik-Tensor (![]() ) von 0 verschiedene Komponenten hat. Dieser hat im Triklinen 6 freie Parameter
) von 0 verschiedene Komponenten hat. Dieser hat im Triklinen 6 freie Parameter

In speziellen Kristallsystemen sind nun einige Parameter 0 oder hängen von anderen ab. Im Tetragonalen ist

Im Momoklinen
Am schwierigsten ist der Fall im Triklinen, da hier eine Matrix erzeugt werden muß, die die korrekte Metrik hat, aber auf Dreiecksform gebracht ist.
Es seien ![]() die Längen der (direkten) Basisvektoren und
die Längen der (direkten) Basisvektoren und
![]() die Winkel zwischen ihnen.
die Winkel zwischen ihnen.
Es wird der Basisvektor ![]() parallel zur X-Achse des Laborkoordinantensystems definiert
parallel zur X-Achse des Laborkoordinantensystems definiert
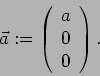
![]() soll in der X-Y-Ebene liegen
soll in der X-Y-Ebene liegen
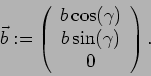
Da
![]() ist, da
ist, da ![]() , gilt
, gilt
![]() . Analog folgt aus
. Analog folgt aus
![]() und damit
und damit
![]() .
. ![]() wird aus der Länge von
wird aus der Länge von ![]() bestimmt. Also ist
bestimmt. Also ist
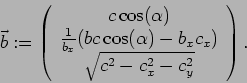
Dies ist die direkte Orientierungsmatrix ![]() . Die reziproke erhält man mit
. Die reziproke erhält man mit
Nun können Nebenbedingungen für die einzelnen Kristallsysteme definiert werden.
Ralf Mueller 2004-04-16