Berechnung der Winkel-Position

Abbildung: Ewaldkonstruktion für beliebige Rotationsachse und Primärstrahlrichtung

Für die Berechnung einer Winkel-Position, in der die Beugungsbedingung erfüllt ist, muß die Ewald-Kugel mit einem Kreis geschnitten werden. Hierfür wird eine Basistransformation gemacht, mit der sowohl der Beugungsvektor als auch der einfallende Strahl transformiert wird. Die neue Basis hat einen Vektor in Richtung der Rotationsachse, einen zweiten in Richtung des $\vec{h}$-Vektors abzüglich der ersten Komponente und einen dritten senkrecht zu den beiden anderen.

$$\vec{B}_3=\vec{r}$$

$$\vec{B}_1=\vec{h}-\vec{h}\vec{r}\frac{\vec{r}}{\vert\vec{r}\vert}$$

$$\vec{B}_2=\vec{B}_1\times\vec{B}_2.$$

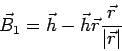
Die Vektoren sind zu normieren.

In dieser Basis ist nun $hr:=h_z'$ die Projektion des $\vec{h}$-Vektors auf die Rotationsachse. $r_0:=h_x'$ ist die Länge des $\vec{h}$-Vektors in der Ebene senkrecht zur Rotationsachse (in der sich die Rotation abspielt).

Der Abgebeugte Strahl $\vec{s}_1$ soll die Länge $\frac{1}{\lambda}$ haben. Also soll sein:

$$(s_{0x}+h_x)^2+(s_{0y}+h_y)^2+(s_{0z}+h_z)^2=\frac{1}{\lambda^2}$$

mit den Nebenbedingungen:

$$h_z=hr$$

und

$$(h_x^2+h_y^2)=r_0.$$

Dies läßt sich mit Maple lösen, und man erhält die beiden Wertepaare ( $h_{x,1/2},h_{y,1/2}$) (Die jeweiligen zusammengehörenden Vorzeichen muß man anhand der Länge des abgebeugten Strahls testen.

In [4] wird das Intervall des Drehwinkels für eine endliche experimentelle Auflösung (diese wird effektive Mosaizität $EMS$ genannt) für den Fall einer Drehachse parallel zur Y-Achse und einem Primärstrahl parallel zur X-Achse berechnet. Angewandt auf unser Koordinatensystem bedeutet dies:

$$\vec{h}=R(\phi)\mathbf{U}\vec{H}$$

Nun ergeben sich die beiden Positionen, bei denen die Beugungsbedingung erfüllt sind (Eingang und Ausgang der Ewald-Kugel), indem man die erweiterte Beugungsbedingung

$$\vert\vec{h}\vert^2+\frac{2h_{x,1}}{\lambda}-\eta_1<0\mbox{ und } \vert\vec{h}\vert^2+\frac{2h_{x,2}}{\lambda}+\eta_2>0$$

mit $\eta_{1}=\frac{EMS}{\lambda}\sqrt{h_{x,1}^2+h_{y,1}^2}$ und $\eta_{2}=\frac{EMS}{\lambda}\sqrt{h_{x,2}^2+h_{y,2}^2}$
beim Eintritt in die Ewald-Kugel und

$$\vert\vec{h}\vert^2+\frac{2h_{x,1}}{\lambda}-\eta_1>0\mbox{ und } \vert\vec{h}\vert^2+\frac{2h_{x,2}}{\lambda}+\eta_2<0$$

beim Austritt aus der Ewald-Kugel überprüft. $h_{x,1},h_{x,2}$ sind die beiden um die Winkel $\phi_{1,2}$ gedrehten Beugungsvektoren.

Erweitert auf beliebige Rotationsachsen bedeutet dies $\eta$ ist die Länge des Beugungsvektors abzüglich der Projektion auf die Primärstrahlrichtung $\frac{\vec{s}_0}{\vert\vec{s}_0\vert}$.

$$\vec{p}_0=\lambda\vec{s}_0\cdot\vec{h}\cdot\vec{s}_0$$

$$\eta=\vert\vec{h}-\vec{p}_0\vert\frac{EMS}{\lambda}.$$

Nun läßt sich die Beugungsbedingung allgemeiner formulieren:

$$\vert\vec{s}_0+\vec{h}\vert-\frac{1}{\lambda}=0$$

oder inklusive der $\eta$s

$$\vert\vec{s}_0+\vec{h}_1\vert+\eta_1-\frac{1}{\lambda}>0 \mbox{ und } \vert\vec{s}_0+\vec{h}_2\vert-\eta_2-\frac{1}{\lambda}<0$$