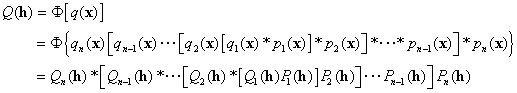 . (6)
. (6)
In the following, we consider only one-dimensionally incommensurate
modulated crystals. The structure of the object is represented by the potential
distribution function, which is now aperiodic and can be considered as
a 3-dimensional hypersection
where
Where a, b and c are the three vectors defining the 3-dimensional unit cell of the basic structure. d is the unit vector along the extra dimension, which is perpendicular to the 3-dimensional physical space, i.e. simultaneously perpendicular to a, b and c. q1, q 2andq3 are components of the modulation wave vector q = q1 a* + q2b* + q 3c* . a*, b* and c* are the three vectors defining the reciprocal unit cell of the basic structure.
In the 4-dimensional reciprocal space, a position vector is expressed as
Where
ai .b j = dij (i, j =1, 2, 3, 4) . (4)
Hence
b1 = (a*, 0) ,
b2 = (b*, 0) ,
b3 = (c*, 0) ,
b4 = (q , d) .
(5)
Suppose that the incident electron beam is parallel to
a1
and that there is no modulation along this direction, i.e.
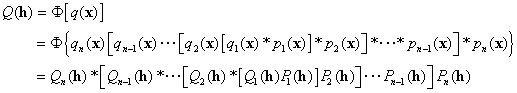 . (6)
. (6)
Where
![]() , (7)
, (7)
Since j j(x2, x3, 0) is an aperiodic function, the multislice calculation will be much more complicated than that for conventional crystalline samples. To avoid the difficulty, We calculate Q(h's) instead of Q(h) .
![]() . (9)
. (9)
Where
![]() , (10)
, (10)
Now Q(h's)
can be calculated similar to that for conventional structures and then
Q(h)
can be obtained by projecting Q(h's)
along
For the reason of simplicity, we will prove only
![]() . (12)
. (12)
Notice that the Fourier transform of a function's projection will be the section of the function's Fourier transform through the origin and perpendicular to the projecting direction. Since
![]() , (13)
, (13)
we have from the left-hand side of equation (12)
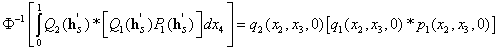 . (14)
. (14)
Hence
![]()
![]() . (15)
. (15)