Multislice method for ordinary crystals
References:
Cowley, J. M. & Moodie, A. F. (1957). Acta Cryst.,
10,
609-619.
Cowley, J. M. (1981). Diffraction Physics, 2nd
ed., pp. 225-247. Amsterdam: North-Holland.
In the multislice approach of dynamical electron diffraction,
the sample is divided into n thin slices perpendicular
to the incident electron beam.
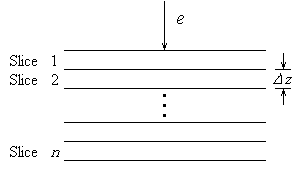
Suppose the incident electron beam is parallel to one
of the crystallographic axis, say
a3,
of the object. Let Dzj
,
jj(x)
and qj(x)
represent respectively the thickness, the projected potential distribution function
and the transmission function of the jth slice. Since
Dzj
is small, each slice can be treated as a phase object. We have
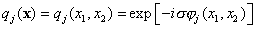 , (1)
, (1)
where
s = p / lU , U is
the accelerating voltage,
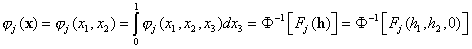 ,
,
F-1 denotes the
operation of inverse Fourier transform,
Fj(h) is the 2-dimensional structure
factor of the jth slice.
Since the electron wavelength is much smaller than the linear
dimension of the object and the distance from the object to the observation
plane, the propagation of electrons through each slice becomes a Fresnel
diffraction. Thus according to the Kirchhoff formula, the wave function
exiting the bottom plane of the first slice is
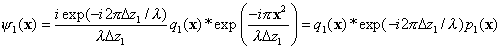 , (2)
, (2)
where
* denotes the operation of convolution
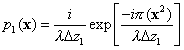 is the propagation factor of the first slice.
For simplicity the factor exp(-i2pDz
j/l)
will be omitted in all wave functions.
Thus, equation. (2) becomes
is the propagation factor of the first slice.
For simplicity the factor exp(-i2pDz
j/l)
will be omitted in all wave functions.
Thus, equation. (2) becomes
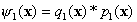 . (3)
. (3)
Accordingly, the wave function on the bottom plane of
the second slice will be
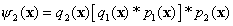 . (4)
. (4)
Finally, the wave function on the bottom plane of the
nth
slice, i.e. the object wave function becomes
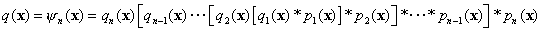 . (5)
. (5)
The diffraction wave function of the object is then the
Fourier transform of equation (5). According to the convolution theorem
it will be
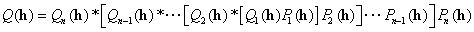 , (6)
, (6)
where
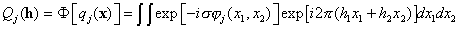
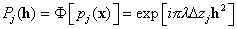 ,
,
F denotes the operation of
Fourier transform.

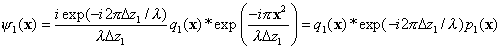 , (2)
, (2)
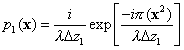 is the propagation factor of the first slice.
is the propagation factor of the first slice.