RMCA Program
Reverse Monte Carlo (RMC) is a method for producing three dimensional models of the structure of disordered materials that agree quantitatively with available diffraction data. RMC use the total scattering (Bragg + diffuse) and not only distinct features like peak positions. It is a variation of the standard Metropolis Monte Carlo (MMC) but without use of an interatomic potential (except maybe a hard core potential, which keep atoms from overlapping). Different types of data, for example neutron and X-ray diffraction, can be modelled at the same time.
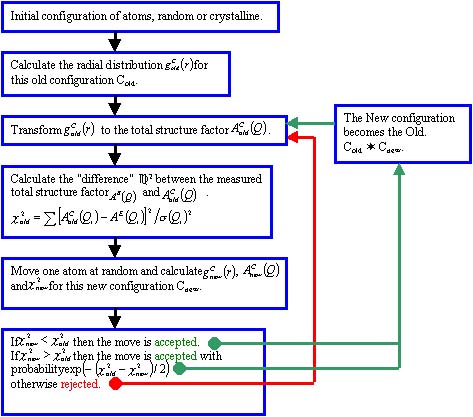
A configuration of atoms in a box with periodic boundary conditions is used in the modelling. The pair distribution function gC(r) and total structure factor AC(Q) of the configuration are calculated and compared to the experimentally determined functions gE(r) or AE(Q). The atoms in the box are moved randomly and after each move AC(Q) is compared to AE(Q) (or gC(r) is compared to gE(r)) and a decision is made to accept or reject the move. See the RMC flowchart.
Two ways exist for running RMC with neutron data; the first is to fit gC(r) to gE(r). This requires that gE(r) is known to relatively high r-values. The program MCGR can be used for this purpose, it is described here. The second method is to fit AC(Q) to AE(Q); since our configuration box is finite with a box length L and out sample in practise is infinite we have to convolute AE(Q) with a step function that is unity for r < L/2 and zero for r > L/2 before using it with RMC.
A number of constraints can be used during the RMC modelling of the configuration. The most commonly used, is on the closest distance of approach of two atoms. We may have chemical information of bond length that forbids atoms to come to close. For each pair of atom types we can include a closest approach distance.
The second most commonly used constraint is on the coordination of atoms. A coordination number na b is defined as being the number of atoms of type b between two fixed distances, of one of type a . Multiple coordination numbers can be included.
From the modelled configuration we can obtain information like partial pair distribution functions, angular distributions and see where atoms are likely to be found. To download programs click here.
RMC Flowchart

![]()