| Glazer's Concept | Structural Criteria | Perovskites - Overview | Homepage |
The tolerance factor inventend for the perovskite structure by Goldschmidt takes simply into account, that three types of spheres in a perovskite-structure, will have contact each other. Since the ionic radii are generally known quite well, a tolerance factor can be calculated, that indicates the "compatibitly" of a given set of ions with the ideal, cubic perovskite structure.
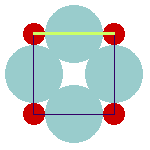
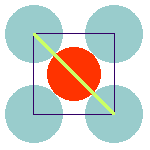
The anion-cation contacts in the ideal cubic pervoskite and their relation to the lattice parameter are shown here:


The anions separate both, the A-cations and the B-cations. The lattice constant is determined by the sum of the ionic diameters of the anion and the B-cation, as is shown in the left figure. At the same time, the sum of the diameters of anion and A-cation determines the plane diagonal (which equals —2) times the lattice constant; cf. right figure).
Thus, a condition to yield the ideal perovskite is
The introduction of factor t, that is simply the ratio of the equation's left side and it#s right side, leads to the definition for Goldsschmidt's tolerance factor:
| t | = |
|
|---|
Once we have introduced t, we can try to find out what happens, when it differs from the ideal value:
Tolerance Factor t ‚ Validity Ranges and Corresponding Perovskite Variants
| t-value | Effect | Possible Structures |
|---|---|---|
| > 1 | A-cations are too large to fit into their interstices | Hexagonal perovskite polytypes |
| ~0.9 ... 1.0 | Ideal conditions | Cubic perovskites |
| 0.71 ... 0.9 | A-cations are too small to fit into their interstices | Several possible structures. Among them:
|
| < 0.71 | A-cations are of same size as B-cations ( 1/—2 = 0.71 ) | Possible close-packed structures
|
| Back to Top | Glazer's Concept | Structural Criteria | Perovskites - Overview | Homepage |