Euler Angles

[Euler angles] - [Rotation matrices]
[Conventions] - [References]
[Go Home]  

Euler Angles

The triplet of Euler angles (a, b, g) is useful to describe rotations or relative orientations of orthogonal coordinate systems. Unfortunately, their definition is not unique and in the literature there are as many different conventions as authors. The convention employed here is one of the more common ones [1]. All rotations are in a counter-clockwise fashion (right-handed, mathematically positive sense).

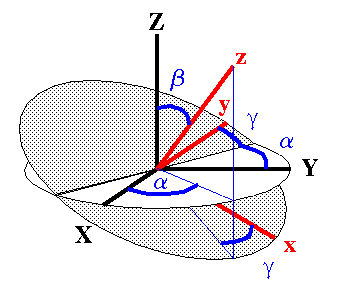The Euler angles (a, b, g) relate two orthogonal coordinate systems having a common origin. The transition from one coordinate system to the other is achieved by a series of two-dimensional rotations. The rotations are performed about coordinate system axes generated by the previous rotation step (the step-by-step procedure is illustrated in the topic Rotation Matrices). The convention used here is that a is a rotation about the Z axis of the initial coordinate system. About the y' axis of this newly generated coordinate system a rotation by b is performed, followed by a rotation by g about the new z axis.

Given the Euler angles, the step-by-step procedure illustrates how to move from one coordinate system to the other. However, given the two coordinate systems, how can one determine the Euler angles relating them? This is described in the topic Determining Euler Angles.

The usual ranges for a, b, g are:

   0 <= a <= 360

   0 <= b <= 180

   0 <= g <= 360

Rotation Matrices

Rotations or transformations from one coordinate system into another are conveniently described by the triplet of Euler angles. Using the Euler angles, this three-dimensional problem can be dissected into a sequence of two-dimensional rotations, whereby in each rotation one axis remains invariant.

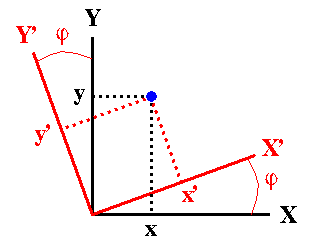2D Analogy:

In order to simplify the problem, let us start with a two-dimensional rotation:

Suppose the coordinates, (x,y), of a point in the two-dimensional XY system are known, but we are actually interested in knowing the coordinates of this point in another coordinate system, X'Y', which is related to the XY system by a counter-clockwise rotation by an angle j.

As the figure indicates, the coordinates of the given point in the new coordinate system will be:

   x' = x cos j + y sin j

   y' = -x sin j + y cos j

or, in matrix notation: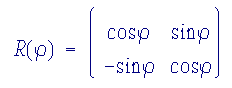

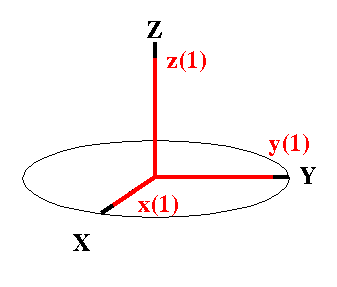Start: Coincidence

Now, transferred to a three-dimensional problem, the goal will be to describe the coordinates in a final rotated system (x,y,z) which is related to some initial coordinate system (X,Y,Z) by the Euler angles. The final system is developed in three steps, each step involving a rotation described by one Euler angle. At the start, both coordinate systems, (X,Y,Z) and (x(1), y(1), z(1)), shall be coincident.

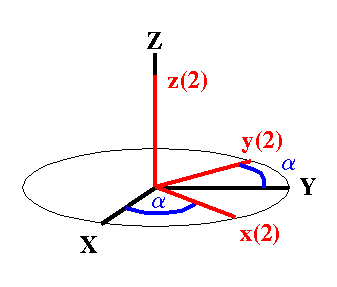1st Rotation

The first rotation involves the Euler angle a. The x(1), y(1), z(1) axis system is rotated about the Z axis through an angle a counterclockwise relative to X,Y,Z to give the new system x(2), y(2), z(2). It is clear from the figure that this rotation mixes the coordinates along X and Y, completely analogous to the two-dimensional rotation described above, while the coordinate along Z remains unaffected. The rotation matrix to describe this operation is given by: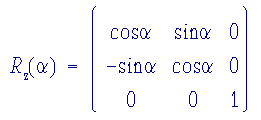

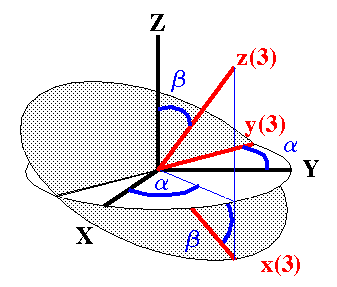2nd Rotation

The second rotation involves the Euler angle b. The x(2), y(2), z(2) axis system is rotated about the y(2) axis through an angle b counterclockwise to generate the new coordinate system x(3), y(3), z(3). Analogous to the first Euler rotation, this mixes the coordinates along x(2) and z(2), while the coordinate along y(2) remains unaffected. This operation also generates a line of nodes parallel to the direction of y(2). The rotation matrix to describe this operation is given by: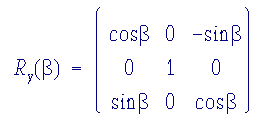

3rd Rotation

The last rotation involves the Euler angle g. The x(3), y(3), z(3) axis system is rotated about the z(3) axis through an angle g counterclockwise to generate the final coordinate system x, y, z. Analogous to the first Euler rotation, this mixes the coordinates along x(3) and y(3), while the coordinate along z(3) remains unaffected. The rotation matrix to describe this operation is given by: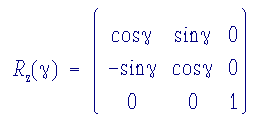

The combined effect of these three rotations is given by this transformation matrix:

Conventions

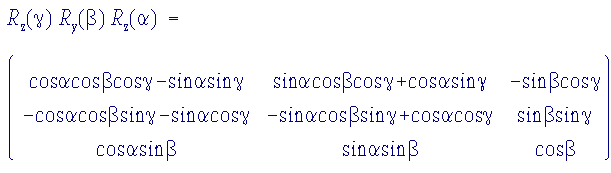
Unfortunately, there are different conventions for the Euler angles relating two coordinate systems:

Note that rotation about sequentially newly generated axes produces the same result as rotations by the same angles about the fixed original axes (cf. Mehring's book, appendix [4]).

References

[1]  M. E. Rose, Elementary Theory of Angular Momentum, Wiley: New York 1957.
[2]  G. Arfken, Mathematical Methods for Physicists, 3rd. ed., Academic Press: New York 1985.
[3]  H. W. Spiess, In NMR Basic Principles and Progress; P. Diehl, E. Fluck, R. Kosfeld, Eds.; Springer Verlag, Berlin, 1978, Vol. 15.
K. Schmidt-Rohr, H. W. Spiess, Multidimensional Solid-State NMR and Polymers, Academic Press: London 1994.
[4]  M. Mehring, Principles of High Resolution NMR in Solids; 2nd ed.; Springer-Verlag, Berlin, 1983.
[5]  K. Narita, J.-I. Umeda, H. Kusumoto, J. Chem. Phys. 1966, 44, 2719.
[6]  D. Freude, J. Haase, In: NMR Basic Principles and Progress; P. Diehl, E. Fluck, H. Guenther, R. Kosfeld, J. Seelig, Eds.; Springer Verlag, Berlin, 1993, Vol. 29.
[7]  J. L. Dye, A. S. Ellaboudy, J. Kim, Solid State NMR of Quadrupolar Nuclei; In: "Modern NMR Techniques and Their Application in Chemistry", Practical Spectroscopy Series Vol. 11; A. I. Popov, K. Hallenga, Eds.; Marcel Dekker, Inc., New York, 1991, pp 217-322.
[8]  Stauss, J. Chem. Phys. 1967, 40, 1988.
[9]  J. F. Baugher, P. C. Taylor, T. Oja, P. J. Bray, J. Chem. Phys. 1969, 50, 4914.
[10]  H. Goldstein, Classical Mechanics, 2nd. ed.; Addison-Wesley, Reading, MA, 1980.
[11]  W. P. Power, R. E. Wasylishen, S. Mooibroek, B. A. Pettitt, W. Danchura, J. Phys. Chem. 1990, 94, 591.

[ Go Home ] | last modified: 20.06.2002