Sigmas

Experimentell ermittelt man die integrale Intensität durch Summation über den Reflexbereich, abzüglich des Untergrundes. Letzterer wird für Scans mit einem Punktdetektor aus den Flanken des Reflexes ermittelt, für Flächenzähler aus den Pixeln in der Umgebung des Reflexes. Wenn $n_p$ die Zahl der Schritte oder Pixel im Reflex und $n_b$ die Zahl der Schritte oder Pixel im Untergrund ist, dann gilt für die integrale Intensität $I_{obs}$ und ihre Varianz $\sigma^2(I_{obs})$:

$$I_{obs} = I_p - \frac{n_p}{ n_b} I_b,$$

$$\sigma^2_{c_t} = I_p + \left(\frac{n_p}{n_b}\right)^2 I_b.$$

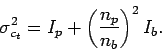
Der Fehler enthält nur den Beitrag aus der Zählstatistik (,,Poisson-Statistik``). Für schwache Reflexe macht er den wesentlichen Anteil des Gesamtfehlers aus. Besonders für starke Reflexe, für die $\sigma(I)$ durch Erhöhung der Meßzeit prinzipiell beliebig klein gemacht werden kann, ist er nur einer von vielen Beiträge zum Meßfehler:

$$\sigma^2 = \sigma^2_{ct} +\sum_i\sigma_i^2,$$

wobei $\sigma_{ct}$ der Beitrag aus der Zählstatistik, $\sigma_i$ der Beitrag der $i$-ten Fehlerquelle ist. Macht man nun die plausible Annahme, daß Meßfehler proportional zur integralen Intensität sind, dann gilt:

$$\sum_i\sigma_i^2=\sum_i(p_i\cdot I_{obs})^2=p^2\cdot I_{obs}^2,$$

mit $p^2 = \sum p_i^2$. Daher hat der Meßfehler die Form

$$\sigma^2 = \sigma_{ct}^2 + p^2 \cdot I^2_{obs}.$$

Der Parameter $p$ ist typisch für ein gegebenes Diffraktometer und die gewählten Datensammlungsparameter. Sofern der Kristall von guter Qualität ist, also selber keinen signifikanten Beitrag zum Fehler liefert, ist dieser Parameter für eine gegebene Apparatur konstant, weshalb er auch als ,,Diffraktometerkonstante`` bezeichnet wird. Übliche Werte dieser Diffraktometerkonstanten liegen bei bei $0,02,\ldots,0,04$. Die Bedeutung von $p$ ist recht einfach: kein Reflex kann besser als auf $100\cdot p$ % gemessen werden. Für die starken Reflexe macht der Beitrag des zweiten Terms der letzten Gleichung praktisch den gesamten Fehler aus.

Diese für Einkristalldiffraktometer mit Punktzähler inzwischen allgemein akzeptierte Vorgehensweise (obiges Gewichtssystem ist z.B. Standard in SHELX) läßt sich ohne weiteres auf Daten von Flächendetektoren übertragen. Das Auslesen erfolgt über einen Photomultiplier und unterliegt deshalb der Poisson-Statistik. Weitere Fehlereinflüsse sind gegebenenfalls ortsabhängig, so daß man es nicht mehr mit einer einzigen Konstanten $p$ zu tun hat. Vielmehr wird es einen konstanten und einen mit dem Ort variierenden Beitrag zur ,,Diffraktometerkonstanten`` geben:

$$p^2 = p^2_o + p^2(x,y,z).$$

Wie der variable Anteil aussieht, das gilt es eben herauszufinden. Das ist durchaus möglich, wenn man wiederholte Messungen ein und desselben Reflexes oder die Intensität symmetrisch äquivalenter Reflexe miteinander vergleicht. Aus der Streuung um den Mittelwert kann man die tatsächliche Varianz $\sigma^2_{av}(I)$ der Einzelmessung erhalten und sie mit der Varianz $\sigma^2_{ct}(I)$ aus der Poisson-Staistik vergleichen. Aus ihrer Differenz erhält man einen Schätzwert für $p$:

$$p^2\approx\frac{\sigma^2_{av}-\sigma^2_{ct}}{I^2_{obs}}.$$

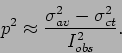
Mittelung über genügend äquivalente Reflexe gibt dann einen plausiblen Wert für $p$. Sofern $p$ -- wie man für einen Flächenzähler erwarten kann -- ortsabhängig ist, muß man diese Bestimmung halt in Abhängigkeit vom Ort durchführen.

Zu Beginn ist das sicher ein aufwendiges Programm; wenn man aber einmal die ,,Diffraktometerkonstante`` (ggf. ortsabhängig) kennt, dann kann man in Zukunft diesen Wert auch für weitere Messungen verwenden. Sollte für eine Messung einmal $p$ deutlich größer sein als normal üblich, dann deutet das auf Probleme mit der Messung hin; in der Regel liegt es an der unzureichenden Probenqualität.