For details of the superspace description of incommensurate structures the reader is referred to the papers by de Wolff (1974, 1977), Janner, Janssen & de Wolff (1983), Yamamoto (1982) and van Smaalen (1992). In the following only a brief description is given.

        For one-dimensionally modulated structures, there is only one kind of modulation waves, which have a common wave vector

,    (1)

where a*, b*, c* are vectors defining the reciprocal lattice of the basic structure. Since the modulation is incommensurate, at least one of the components, q₁, q₂ and q_3, should be irrational. The position vector of a Bragg reflection is thus

,    (2)

where h, k, l, m are all integers, m = 0 for main reflections, m ¹ 0for satellites.We can imagine that q is the projection of a 4-dimensional vector onto the 3-dimensional physical space. Therefore we can construct a 4-dimensional reciprocal lattice having basic vectors

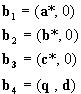,    (3)

where d is a unit vector perpendicular to the 3-dimensional physical space. According to the reciprocal relationship

(i, j =1, 2, 3, 4) ,     (4)

the basic vectors of the corresponding 4-dimensional direct lattice should be

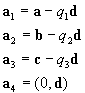.    (5)

From equation (3) the position vector of a reflection in the 4-dimensional reciprocal space becomes

,    (6)

where h₁ = h, h₂ = k, h₃ = l, and h₄ = m. From equation (5) the position vector of a point in a 4-dimensional unit cell in direct space is

,    (7)

where x_{1 ,} x_{2 ,} x₃ and x₄ are fractional coordinates. The diffraction pattern of an incommensurate one-dimensionally modulated structure corresponds to the projection of a 4-dimensional reciprocal lattice. The incommensurate structure itself can be obtained by cutting a 4-dimensional periodic structure perpendicular to the vector d. A hypersection in the 4-dimensional direct space perpendicular to the vector d satisfies

.    (8)

According to Equation (5) we have

.    (9)

Defining

,    (10)

the 4-dimensional periodic structure may also be described using a , b , c and d as the basic vectors. Position vectors in a 4-dimensional unit cell in direct space is thus

,    (11)

where x, y, z and t are fractional coordinates. Values of x, y, z with respect to the basic vectors a, b, c are respectively the same as x_1, x_2, x₃ with respect to basic vectors a₁, a₂, a₃. A one-dimensionally incommensurate modulated structure in 3-dimensional physical space is described by the corresponding 4-dimensional periodic structure on the hypersection at t = 0. 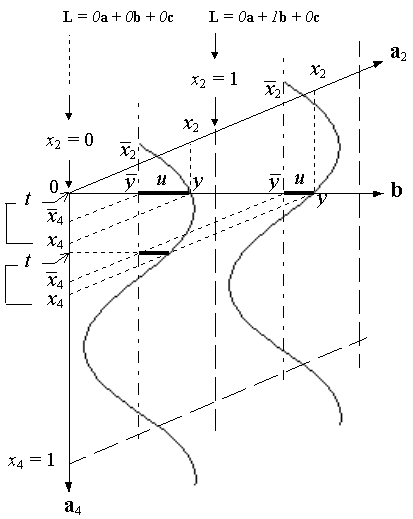Parameters of a modulated atom on the hypersection at t = 0 can be expressed with respect to their average values. The following figure shows how the parameter y is related to its average value  and the modulation function . The two curves represent two identical atoms in two adjacent unit cells in superspace. The y component of the atomic position is modulated along the direction x₄ as shown by the curve.

For any particular parameter we can write

,    (12)

or according to equations (1) and (9) we have equivalently

, (13)

where m denotes the m^th atom in a unit cell of the basic structure, is the average parameter, which equals for positional parameters or equals for occupational/substitutional and thermal parameters, L is a lattice vector of the basic structure,  is the average parameter in the unit cell with its origin at L = 0, u is the modulation function with period equal to unity,  is the fourth coordinate of a point in 4-dimensional space having its first three coordinates respectively equal to the average coordinates ,  and , q is the modulation wave vector,  is the average position vector of the m^thatom, is the average position vector in the unit cell at L = 0. The modulation function u can be expanded into a Fourier series

.    (14)

Hence atomic coordinates can be expressed as a Fourier series with its zero order coefficient equal to the corresponding average coordinate, i.e.

,    (15)

where .

        The structure-factor formula for a one-dimensionally modulated structure is

,    (16)

where

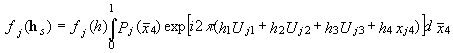.    (17)

The f_j(h) on the right-hand side of (17) is the ordinary atomic scattering factor, P_j is the occupational modulation function and U_j describes the deviation of the j^th atom from its average position . For more details on (16) and (17) the reader is referred to the papers by de Wolff (1974), Yamamoto (1982) and Hao, Liu & Fan (1987). What should be emphasised here is that, according to (16) a modulated structure can be regarded as a set of ‘modulated atoms’ situated at their average positions in 3-dimensional space. The ‘modulated atom’ in turn is defined by a ‘modulated atomic scattering factor’ expressed as (17).

References
        Hao, Q., Liu, Y. W. and Fan, H. F. (1987). Direct methods in superspace I. Preliminary theory and test on the determination of incommensurate modulated structures, Acta Cryst. A43, 820-824.
        Janner, A. Janssen, T. and Wolff, P. M.de (1983). Bravais classes for incommensurate crystal phases, Acta Cryst. A39, 658-666.
        Wolff, P. M. de (1974). The pseudo-symmetry of modulated crystal structures, Acta Cryst. A30, 777-785.
        Wolff, P.M. de (1977). Acta Cryst. A33, 493-497.
        Yamamoto, A. (1982). Structure factor of modulated crystal structures, Acta Cryst. A38, 87-92.
        Smaalen, S. van (1992). Superspace description of incommensurate intergrowth compounds and the application to inorganic misfit layer compounds, Mater. Sci. Forum 100 & 101, 173-222.